Interval, Pertidaksamaan, Dan Nilai Mutlak - Hallo sahabat jinklink, Pada Artikel yang anda baca kali ini dengan judul Interval, Pertidaksamaan, Dan Nilai Mutlak, kami telah mempersiapkan artikel ini dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Kalkulus, yang kami tulis ini dapat anda pahami. baiklah, selamat membaca.

Judul : Interval, Pertidaksamaan, Dan Nilai Mutlak
link : Interval, Pertidaksamaan, Dan Nilai Mutlak

Interval, Pertidaksamaan, Dan Nilai Mutlak

Sistem Bilangan Real

Ilustrasinya

Garis Real

1. R diasosiasikan sebagai garis lurus

    x anggota dari R diasosiasikan sebagai suatu titik di garis

   

2. Titik acuan: bilangan 0

     Bilangan real positif x terletak x unit di kanan 0 

     Bilangan real positif -x terletak x unit di kiri 0 

Urutan

Definisi (Relasi Urutan)

1. Relasi urutan < (dibaca lebih kecil daripada) didefinisikan oleh 

    x < y jika dan hanya jika y - x positif. 

2. Relasi urutan <= (dibaca lebih kecil daripada atau sama dengan)
didefinisikan oleh 

    x <= y jika dan hanya jika y - x positif atau nol

Sifat-Sifat Urutan

1. Trikotomi

    Jika x dan y adalah bilangan-bilangan, maka tepat satu di antara
yang berikut berlaku:

    x < y atau x = y atau x > y

2. Ketransitifan

    Jika x < y dan y < z, maka x < z  

3. Penambahan

    x < y jika dan hanya jika x + z < y + z

4. Perkalian

    Ketika z positif, x < y jika dan hanya jika xz < yz
    Ketika z negatif, x < y jika dan hanya jika xz > yz 

Interval 

Definisi (Interval)

Interval adalah himpunan bilangan real yang didefinisikan dan
dilambangkan sebagai berikut

Gabungan dan Irisan

Definisi

Misalkan A dan B merupakan interval

Pertidaksamaan

Definisi (Pertidaksamaan)

Pertidaksamaan adalah pernyataan matematik yang memuat salah satu

relasi urutan <, >, <= , atau >= .

Definisi (Penyelesaian Pertidaksamaan)

Penyelesaian pertidaksamaan adalah semua bilangan real yang memenuhi
pertidaksamaan tersebut

Menyelesaikan pertidaksamaan:

• Dengan sifat urutan
• Dengan garis bilangan bertanda 

Nilai Mutlak 

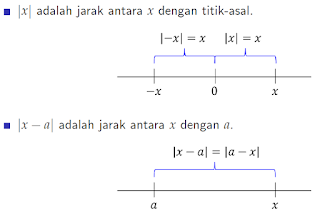
Definisi (Nilai Mutlak)

Nilai mutlak suatu bilangan real x, dinyatakan oleh |x|, didefinisikan
sebagai 

 yang perlu di perhatikan:

Sifat-Sifat Nilai Mutlak

1. Misalkan a, b anggota R dan n anggota Z, maka

2. Misalkan x, y anggota R dan a > 0, maka

3. Misalkan x, y anggota R dan n anggota Z, maka

Semoga Bermanfaat 

Demikianlah Artikel Interval, Pertidaksamaan, Dan Nilai Mutlak

Sekianlah artikel Interval, Pertidaksamaan, Dan Nilai Mutlak kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.

Anda sekarang membaca artikel Interval, Pertidaksamaan, Dan Nilai Mutlak dengan alamat link https://jinklink.blogspot.com/2016/07/interval-pertidaksamaan-dan-nilai-mutlak.html