Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1] - Hallo sahabat jinklink, Pada Artikel yang anda baca kali ini dengan judul Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1], kami telah mempersiapkan artikel ini dengan baik untuk anda baca dan ambil informasi didalamnya. mudah-mudahan isi postingan Artikel Kalkulus, yang kami tulis ini dapat anda pahami. baiklah, selamat membaca.
Judul : Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1]
link : Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1]
Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1]
Mengapa turunan penting?
Pemahaman yang baik tentang konsep turunan fungsi akan memudahkan memahami laju perubahan suatu variabel yang bergantung pada variabel lain, misalnya penentuan
Turunan Fungsi
Turunan Fungsi pada Suatu Titik/Bilangan
Definis turunan fungsi pada suatu titik
Bila limit tersebut ada (bukan $\infty$ atau $-\infty$), maka fungsi f dikatakan terturunkan (memiliki turunan, differentiable) di a.
Perhatikan gambar (a) berikut:
Ilustrasi geometris definisi turunan pada titik.
Alternatif Formula Turunan
Jika pada definisi diambil x = a + h, maka diperoleh alternatif formula sebagai berikut:
dapat di lihat pada gambar di atas bagian (b)
Turunan Sebagai Kemiringan Garis Singgung
Ilustrasi geometris persamaan garis singgung
Turunan Sebagai Fungsi
Tafsiran Lain Turunan
Notasi Lain Turunan
Misalkan y = f (x).
Beberapa notasi yang menyatakan turunan f
Catatan: notasi dy/dx, df/dx, d/dx hanya merupakan simbol, bukan merupakan operasi pembagian.
Aplikasi Turunan [Fisika: Kecepatan sesaat]
2) Laju objek pada saat t = a adalah |f '(a) |, yakni nilai mutlak kecepatan sesaat.
Aplikasi Turunan [ Ekonomi, Demografi]
bermakna laju total biaya produksi terhadap banyaknya barang (Rp/ton). f '(x) dikenal sebagai biaya marjinal.
Kaitan Turunan dan Kekontinuan
Tidak fungsi tidak mempunya turunan apabila, seperti gambar di bawah ini.
Rumus-Rumus Turunan
Rumus Turunan
Rumus-rumus turunan berikut, dapat diperoleh melalui de.nisi turunan.
Teorema turunan fungsi
Misalkan u = f(x), v = g(x), dan c merupakan suatu konstanta. Maka:

Turunan Fungsi Sesepenggal
Teorema berikut memudahkan dalam mencari turunan fungsi sesepenggal (piecewise functions), tanpa menggunakan definisi turunan.
Teorema [Turunan fungsi sesepenggal]
Turunan Fungsi Trigonometri
Limit penting
$\lim_{\theta \rightarrow 0}\frac{sin \theta }{\theta }=1$
$\lim_{\theta \rightarrow 0}\frac{1-cos \theta }{\theta }=0$
Turunan Sinus Cosinus
$\frac{\mathrm{d} }{\mathrm{d} x}sin x = cos x$
$\frac{\mathrm{d} }{\mathrm{d} x}cos x = -sin x$
Turunan Fungsi Trigonometri
Turunan dari trigonometri sebagai berikut:
Baca juga lanjutan tentang turunan DISINI
Semoga Bermanfaat
Pemahaman yang baik tentang konsep turunan fungsi akan memudahkan memahami laju perubahan suatu variabel yang bergantung pada variabel lain, misalnya penentuan
- Laju pertumbuhan suatu populasi (manusia, ikan, harimau, bakteri,dsb.)
- Biaya marjinal suatu produk.
- Kecepatan mobil seorang pembalap pada suatu waktu tertentu.
- Laju perubahan kecepatan aliran darah berdasarkan jarak dengan dinding pembuluh
- Laju penyebaran informasi, gosip.
- Laju peluruhan bahan radioaktif.
Turunan Fungsi
Turunan Fungsi pada Suatu Titik/Bilangan
Definis turunan fungsi pada suatu titik
Turunan fungsi f pada titik/bilangan a dinyatakan dengan f'(a), adalah
asalkan limit tersebut ada
Bila limit tersebut ada (bukan $\infty$ atau $-\infty$), maka fungsi f dikatakan terturunkan (memiliki turunan, differentiable) di a.
Perhatikan gambar (a) berikut:
Ilustrasi geometris definisi turunan pada titik.
Alternatif Formula Turunan
Jika pada definisi diambil x = a + h, maka diperoleh alternatif formula sebagai berikut:
dapat di lihat pada gambar di atas bagian (b)
Turunan Sebagai Kemiringan Garis Singgung
- Garis singgung pada kurva y = f (x) di titik (a, f (a)) adalah garis yang melalui (a, f (a)) yang kemiringan/gradiennya sama dengan f '(a), yakni turunan f di x = a.
- Persamaan garis singgung pada kurva y = f (x) di titik (a, f (a)) adalah y - f(a) = f '(a) (x - a)
Ilustrasi geometris persamaan garis singgung
Turunan Sebagai Fungsi
- 1. Ganti titik tetap a dengan variabel x pada definisi turunan
- dan sehingga akan diperoleh fungsi f ' dengan
- 2. f ' pada turunan diatas merupakan suatu fungsi, disebut turunan pertama fungsi f .
- 3. Daerah asal f', Df ' = {x : f ' (x) ada}
- 4. Nilai f '(a) juga dapat dihitung dari turunan di atas kemudian mengevaluasi f '(x)
untuk x = a.
Tafsiran Lain Turunan
Notasi Lain Turunan
Misalkan y = f (x).
Beberapa notasi yang menyatakan turunan f
Catatan: notasi dy/dx, df/dx, d/dx hanya merupakan simbol, bukan merupakan operasi pembagian.
Aplikasi Turunan [Fisika: Kecepatan sesaat]
- Nilai f '(a) merupakan laju perubahan sesaat dari y = f (x) terhadap x di x = a.
- Misalkan s = f (t) menyatakan fungsi posisi suatu objek pada waktu t,
2) Laju objek pada saat t = a adalah |f '(a) |, yakni nilai mutlak kecepatan sesaat.
Aplikasi Turunan [ Ekonomi, Demografi]
- Misalkan C = f (x) menyatakan total biaya produksi (Rp) untuk menghasilkan x barang (ton),
bermakna laju total biaya produksi terhadap banyaknya barang (Rp/ton). f '(x) dikenal sebagai biaya marjinal.
- Misalkan P = f (t) menyatakan banyaknya populasi penduduk Indonesia pada waktu t (tahun),
Kaitan Turunan dan Kekontinuan
Tidak fungsi tidak mempunya turunan apabila, seperti gambar di bawah ini.
Rumus-Rumus Turunan
Rumus Turunan
Rumus-rumus turunan berikut, dapat diperoleh melalui de.nisi turunan.
Teorema turunan fungsi
Misalkan u = f(x), v = g(x), dan c merupakan suatu konstanta. Maka:

Turunan Fungsi Pangkat
Teorema turunan fungsi pangkatJika n sembarang bilangan real, maka
Turunan Fungsi Sesepenggal
Teorema berikut memudahkan dalam mencari turunan fungsi sesepenggal (piecewise functions), tanpa menggunakan definisi turunan.
Teorema [Turunan fungsi sesepenggal]
Andaika f kontinu di a serta $\lim_{x\rightarrow a^{-}}f'(x)$ dan $\lim_{x\rightarrow a^{+}}f'(x)$ ada. Fungsi f terturunkan di a jika dan hanya jika $\lim_{x\rightarrow a^{-}}f'(x)$ = $\lim_{x\rightarrow a^{+}}f'(x)$ dan $f'(a)=\lim_{x\rightarrow a^{-}}f'(x)=\lim_{x\rightarrow a^{+}}f'(x)$
Turunan Fungsi Trigonometri
Limit penting
$\lim_{\theta \rightarrow 0}\frac{sin \theta }{\theta }=1$
$\lim_{\theta \rightarrow 0}\frac{1-cos \theta }{\theta }=0$
Turunan Sinus Cosinus
$\frac{\mathrm{d} }{\mathrm{d} x}sin x = cos x$
$\frac{\mathrm{d} }{\mathrm{d} x}cos x = -sin x$
Turunan Fungsi Trigonometri
Turunan dari trigonometri sebagai berikut:
Baca juga lanjutan tentang turunan DISINI
Semoga Bermanfaat
Demikianlah Artikel Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1]
Sekianlah artikel Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1] kali ini, mudah-mudahan bisa memberi manfaat untuk anda semua. baiklah, sampai jumpa di postingan artikel lainnya.
Anda sekarang membaca artikel Turunan - Turunan Fungsi, Kaitan Antara Turunan dan Kekontinuan Dan Rumus-Rumus Turunan [Part 1] dengan alamat link https://jinklink.blogspot.com/2016/08/turunan-turunan-fungsi-kaitan-antara.html









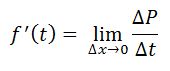



Tidak ada komentar:
Posting Komentar